Quantisweb Software as a tool to optimize an extruder
M’Hammed Mountassir, PhD., Nina Visconti, M.A., Quantisweb Technologies Inc.
Introduction:
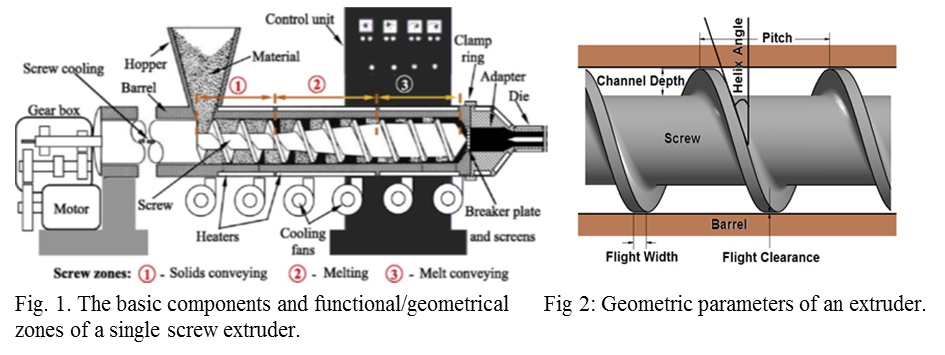
Screw conveying, melting and pressurizing is the backbone of thermoplastics processing. The single screw extruder is the most popular used in the plastics industry (see fig 1 and fig 2). The extruder screw design remains the focus of discussion and research centered on the screw and its components. The one mystery is the helix angle; its complexity is due to its competing requirements such as, a steep angle to resist back pressure flow and a shallow angle to provide the least tortuous path for drag flow. Industries thus follow a ‘rule of thumb’ on the settings of the screw however not necessarily considering the interrelationships of the temperature effect, both from the point of view of melt temperature and energy efficiency [1] and its optimum performance on the final product. In fact, a mathematical model or physical model becomes extremely complex and impossible if one were to incorporate all potential and important parameters and their interactions (see Table 1). To keep the analysis manageable, the mathematical methods applied to date limit the number of parameters and characteristics at any given time.
Table 1. Generally considered parameters:
This paper will summarize the mathematical approaches used in recent years that address the problems associated with the molding process using a ‘single-screw’ extruder. Each of the methods in these approaches are put in context by describing its goals, findings and any eventual or existing limitations. Following the review on the state of the art, a discussion will follow on the use of the Quantisweb methodology, in the context of multi-factor (multivariate) and multi-objective optimization. Finally, we will introduce three examples of how the methodology was used in actual cases and its benefits to the client.
Review:
Among the mathematical methods that have addressed the extrusion process include [2] where the authors used fuzzy logic systems and the Taguchi method based on 3 parameters attempted to optimize a single characteristic of the molding process on the AZ61 magnesium, without showing the optimality of their solution, their work showed a good fit between their modeling and experimental data; or in reference [3] where numerical methods with a discretization of one million finite elements (FEA) are always constraint to understanding the effects of a few specific parameters, such as temperature on molding. Reference [4] personally, I find the most interesting. The authors first do an overview of the studies where the Taguchi method, the RSM (Response Surface Method) and hybrid methods were employed. To address the plastic injection molding process, the authors tried to combine and apply jointly these methods, considering 5 controllable parameters and two characteristics with 5 repetitions, which required 300 experiments. With the resulting behavior laws, they applied multi-objective methods to optimize both characteristics with the MATLAB software for each of the three methods. The results were validated & confirmed after an additional 25 experiments. In the study [5], the use of neural networks is proposed to estimate properties as a function of controllable factors and when a property is binary, it is treated with fuzzy logic and ultimately use genetic algorithms to optimize. All this requires a lot of testing, and it increases as the number of variables and characteristics increase. As for the study ref. [6], a prediction model on the motor consumption of the extruder is discussed under different conditions and different materials without vision of optimality. In ref. [8] simulation studies were carried out to analyze the granulation of plastic mechanism inside a single-screw extruder, considering several parameters which included the friction within the barrel; the model shows a certain analogy with the experimental data without interest in the optimality of the process. While in ref. [7] a large simulation study assisted by expert systems was conducted and funded by 17 companies at a German university to model the molding process by including geometric parameters of the extruder, again, no optimization approach has been effective. In references [9] to [14], stochastic methods have been developed to model a product characteristic (generally the molding) in a dynamic way using time series in their standard form (Box-Jenkins) or their variants to determine the ‘steady state’ process. In ref. [15], the authors studied the influence of design and processing conditions on equipment, using numerical modeling FEA simulation to minutely detail and quantify the particle flow and particle tracking in space and time not only to dynamically capture the flow characterization and size distribution, but also to compare the dispersive and distributive mixing in a twin- flight single screw. The authors infer that the effectiveness of a given extruder can be improved given the ability to define new mixing specifications at various axial cross-sections of the extruder to control the process and equipment scale-up.
The Quantisweb Methodology
The methodology that enables agile product development, has been compared to other methods such as the Taguchi approach, expert systems, neural networks, statistical and/or mathematical software (JMP, Minitab, MATLAB, Mathematica etc.). The outcome of the comparison repeatedly concludes that it is comprehensive, effective and optimal in the local sense (resource minimization) and in the global sense (process optimization and manufacturing process).
Extrusion process for a single-screw.
How do we propose to apply the Quantisweb methodology to the single screw extrusion process? Roughly speaking, the molding process is divided into 3 phases (see Figure 3): the inputs, the extruder, and the outputs. To apply the Quantisweb methodology, each step must be well detailed.
Phase Input:
All controllable parameters (ingredients) and/or processes (speeds, temperatures, etc.) and/or geometric process, with their respective intervals and range must be identified. In addition, identify all the characteristics (uncontrollable) to optimize. The software can handle up to 200 variables (parameters) at once.
Phase Extruder:
As for the extruder, suppose the barrel length of the extruder is equal to L. Then divide this length in m pieces of each length equal to , the number m must be between 50 and 100. It will have (m +1) nodes. In each of these nodes, each product characteristics must be measured individually. For example, for property Yi, the following measurements Yi1,Yi2,…Y(im+1). will be read for each combination of controllable parameter. This approach is used to monitor each of the characteristics over time and space (such as the rate of dissolution of a drug in the blood depending on weather). This measurement will be identified as the result of experiments (ROE) of Quantisweb. The software has the capacity to optimize up to 100 properties simultaneously; MFI to Tensile Strength to Impact Strength to Coefficient of Friction.
Phase Output:
Given the barrel/screw ROE data, we can target the ideal values of all the characteristics and hence optimize the entire process and the extruder process. We then obtain the optimal combination of controllable factors that would optimize all the characteristics of the given product.
Methodology in practical use:
The application provides two approaches in performing optimization: a minimal dynamic design of experiments (mdDOE), where a minimal number of experiments are generated, and data mining, where the data from existing recipes or experiments is reverse engineered. The methodology works from lower data density to whatever density is required to optimize the formula/process with minimum amount of work resulting in the optimal combination of controllable factors and an understanding of the process. The output will either validate the assumptions, and/or highlight the unexpected behavior of the unknown. Furthermore, the application can be used in numerical modeling of Finite Element Analysis and Computational Fluid Dynamics.
Example 1: A minimal dynamic design of experiments (mdDOE) approach got the client to the right level of polymer degradation (chain scission as measured by melt flow index) in a consistent two passes when over the last 10 years it has ranged from two to six passes. The inconsistency had created significant issues with plant capacity and lead times. The problem had resisted at least eight serious attempts at optimization both with and without traditional DOE software assistance. Formulation parameters (catalyst, moisture) were combined with barrel temps (set, actual) and machine operating conditions (feed rate, rpm) to concurrently yield an economically acceptable output rate, machine torque loading and most importantly, a consistent reduced molecular weight as measured by melt flow index. In the end, the problem consisting of 12 parameters was resolved after 13 experiments (np + 1) versus 4096 experiments in a traditional design which would have required two raised to the number of variables (2n).
Example 2: A data mining approach, helped a client optimize an extrusion process in production for over 25 years. Over time, it had become more difficult to meet production targets without increasing levels of rejects and cost. Using production data from 55 recipes, consisting of over 40 variables, 6 die gap constraints, 14 product properties, and 4 process properties was sufficient to restore production quality. During the analysis portion of the project, unexpected behaviors of conflicting relationships and critical variables were discovered. In the end a process with 40 variables and 18 properties was optimized with only 3 experiments that were run on the production line.
Example 3: A minimal dynamic design of experiments (mdDOE) approach was used in a simulation environment using Finite Element analysis (FEA) and Computational Fluid Dynamics (CFD) to help a client reach objectives of lift, drag and minimum pressure coefficient, while designing and optimizing the aerodynamics of a race car. A total of 68 variables (22 continuous and 46 discrete) and 50 constraints (mainly nonlinear: SIN, COS, TAN) were used to generate the (mdDOE). Experiments were run on simulation software. After two months and 310 simulation runs the objectives were reached.
Conclusion:
In this summary, we presented an arsenal of mathematical studies that have examined the extrusion problem using a single-screw extruder during the past 30 years. Subsequently, we presented the approach by Quantisweb methodology to address the same problem, not in a spirit of modeling (understanding what is happening inside the machine) but in a spirit of finding the best combination of controllable parameters to subsequently operate in an optimal environment. Finally, we introduce three examples of the methodology used in practical cases where we clearly demonstrated that the cost and time to bring products to the market were drastically reduced.
References:
[1] Optimization of hot extrusion process for AZ61 magnesium alloy carriers. Su-Hai Hsaiang & all. International Journal of Material Forming (2012) p.259-268.
[2] Numerical investigation of weather strip extrusion forming process by thermal flow analysis. J. R. Cho and J.H. Choi. International Journal advanced Manufacturing Technology (2016).
[3] Optimization of the plastic injection molding process using the Taguchi method, RSM and hybrid GAPSO. Wen- Chin Chen & al. International Journal advanced Manufacturing Technology (2016).
[4] An artificial neural network approach to multiple-response optimization. R. Noorossana & al.
International Journal advanced Manufacturing Technology (2009).
[5] Modelling of Melt Pressure Development in Polymer Extrusion: Effects of Process Settings and Screw Geometry. Chamil Abeykoon and al. Proceedings of 2011 International Conference on Modelling, Identification and Control. Shangai, China, June (2011).
[6] Design and Processing Optimization of Extruder Screws. H. Potente and W. Hanhar. Polymer Engineering and Science (1994).
[7] Investigation of solids Transport in a single screw extruder. P.A Moysey and M.R. Thompson. Polymer Engineering and Science (2004).
[8] On the dynamics and control of a plasticating extruder. Costin M, Taylor & al. Polymer Engineering and Science (1982).
[9] Model reference optimal steady state adaptive computer control of plastics extruder process.
Hassan G. and Farnaby. J . Polymer Engineering and Science (1981).
[10] Adaptive and multivariate control of a single screw extrusion process. Dennis Gemuska D. & al. Can J. Chem Eng (1982).
[11] System identification of date feedback integral observer control of polymer plastic extrusion.
Lin Y and Lee G. Polymer Plast Technol Eng (1997).
[12] Modeling of the plasticating process in a single screw extruder: a fast-track approach.
Lai E and Yu D. Polymer Engineering and Science (2000).
[13] Modelling the effects of operating conditions on motor power consumption in single screw extrusion life system modelling and intelligent computer. Abeykoom C & al. Lecture Notes computer Science (2010).