Quantisweb Methodology as a tool to generate the Optimal Model and solve Problems in Mathematical Simulation.
M’Hammed Mountassir, PhD., Quantisweb Technologies Inc.
Nina Visconti, M.A. Quantisweb Technologies Inc
Introduction:
The first objective of this paper is to present the state of the art in mathematical simulation used in industry. A general background to using simulation is provided followed by the approaches with their respective advantages and disadvantages for any work based on the simulation. The second objective is to introduce the Quantisweb Methodology as an enabler to simulation in selecting and generating an Optimal Model and solving Problems. Then, we will introduce an example of how the methodology was used in an actual case and its benefits to the client. Finally, we will provide useful references to any user who might want to know more.
Simulation Projects:
Simulation projects often involves carrying out a set of activities in preparation for achieving a certain objective. Generally, a given project can be formulated as a multilevel problem and each level is multimodal, each mode is assigned to a certain activity. Ultimately the goal is to attain an optimal solution (in a certain sense of optimality) for all the activities at a reasonable cost and that this solution is stable, robust, and reproducible. Therefore, a project cannot be completed without a detailed description of the subsequent activities, which are generally subject to constraints whether, monetary, human, material, etc.
When a project is constrained, linear or non-linear programming methods used in operational research have proven to be effective, that is, they make it possible to give an explicit solution, when it exists, to the problem raised in its stationary state. However, when the project must deal with a mega system, such as: ordered systems, ATM networks, wireless networks, semiconductors, oriented agents, etc., then, simulation techniques which are in fact an imitation of the state of the system in real time are called upon. (See references [1], [2], [3], [4].)
Mathematical simulation methods can be summarized in two main classes:
The Monte Carlo method and the Trace-Driven method. These methods include the ‘discretization’ and ‘continuation’ of system-related activities. The Monte Carlo method assumes that the data have a certain known probabilistic distribution and therefore the data samples are then generated as per these distributions where this generated data will be used as input data for the simulation model. On the other hand, the Trace-Driven method is based on real data observed on one or more parts of the system, called “trace”. The Trace-Driven approach appears to be more realistic because the data collected reflect all the interactions between the parameters involved. Its great disadvantage is that it requires a lot of repetition. (See references [5]. [6], [7]).
The objectives and limitations of simulation:
Before using simulation tools, one must know what one can expect especially with respect to the mathematical modeling tools.
What simulation can do:
Provide realistic estimates of the expected behavior of a system or variations within the system.
Assess the effects of the following actions:
- Add, move or delete sub-processes.
- Modify the flows within the system.
- Modify process times.
- Introduce or delete new parameters.
- Modify the scheduling and distribution of processes within the system.
- It can only answer questions like: “What happens if …?”.
- It can only reproduce the behavior of the system, once it is modeled.
What simulation cannot do by itself:
- It cannot optimize the performance of a system.
- It cannot therefore produce good results if the modeling of the system is imprecise.
- It does not solve problems; it can only provide indications/inferences from which solutions can be deduced.
The steps of a simulation project:
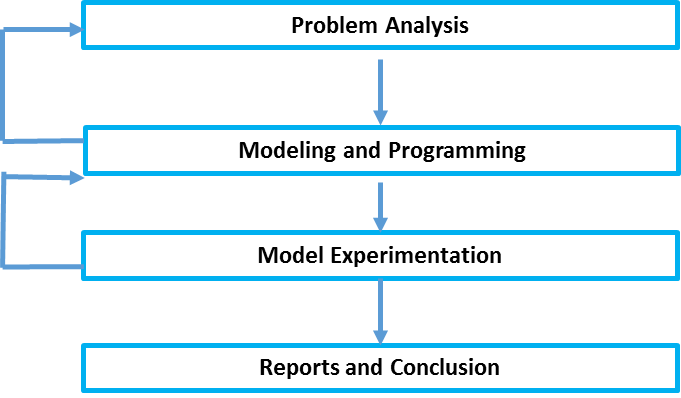
The following diagram (1) describes the steps and feedback involved in a simulation project.
The types of modeling:
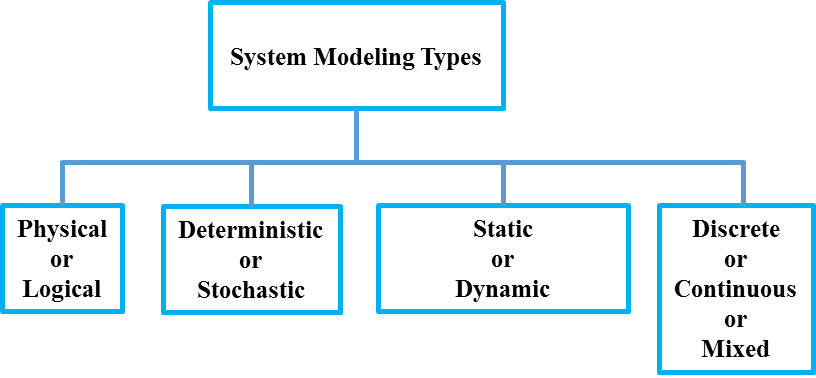
In a mathematical simulation, the user must specify the types of system models beforehand, as shown in the following diagram (2).
Upon entering a simulation study the user must choose only one type of model found in each of the types identified in the schematic diagram (2). Then, the user must choose one of the two simulation methods, Monte Carlo or Trace-driven. It is important to note that this selection restricts the simulation to the selected model and methods and therefore restricting the user from operating the system in an optimal context.
Quantisweb Methodology used to select the Optimal Model and solve Problems;
The Quantisweb methodology easily integrates all these types of models and these simulation methods, providing the user the opportunity to work in real time in the context based on optimal modeling of the whole system. Furthermore, in addition to determine the optimal model, Quantisweb can also solve problems.
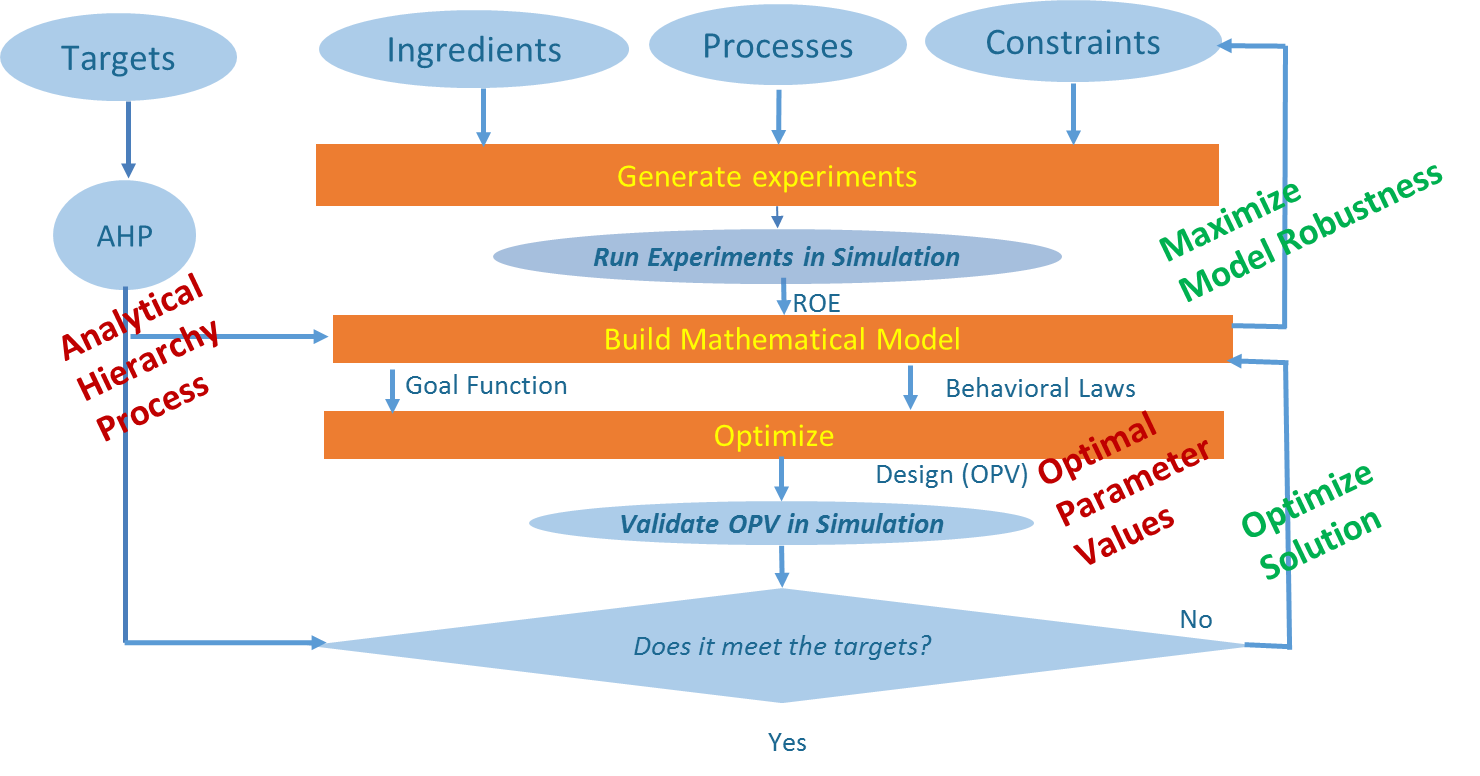
The Quantisweb stochastic-approximation optimization (SAO) process is an integrated approach based on 3 main mathematical methodologies (See reference [8]) that is not only multivariate parameters (X) but also multi-target properties (Y).
The first methodology is the use of a multi-criteria method to order the characteristics of the product as per their importance. This method is based on the principles of hierarchical process analysis (AHP) (See reference (9)).
The second methodology is the use of an arsenal of statistical methods which allow the modeling of each of the characteristics of the product by contenting itself with a minimal DOE (non-factorial). These models are of all possible types (polynomial, logistic, …) linear or non-linear and this according to the information extracted automatically from the results of the experiments (ROE).
The third methodology is an optimization step, where the system receives information from both the user (the ideal values of the properties or the deterministic physical laws) and the information of the two previous modules to establish a multifactorial and multidimensional function to optimize. The system then uses a hybrid optimization library which allows to optimize both random laws and / or deterministic laws simultaneously with or without constraints on the controllable variables, these constraints can be linear or conditional. This step also generates an optimal combination of values for ingredients and process variables that can be validated.
The Quantisweb process:
The Quantisweb process is depicted in the following diagram (3).
Methodology in practical use:
Quantisweb was used to assist in the design of the aerodynamics of a race car to reach objectives of lift, drag and minimum pressure coefficient, while respecting very stringent specifications established by the Society of Automobile Engineers (SAE). This was to be done in a very short period. To meet the objectives, a decision was made to first design and optimize 3 sets of wings, front, middle and rear individually then optimize the aerodynamics of the wings and the car together. The problem included 68 variables (22 continuous and 46 discrete) and 50 constraints (mainly nonlinear: SIN, COS, TAN).
Client feedback:
Using High Performance Computing (HPC) resources, solving large-scale 3D CFD problems has become more viable in recent years. The use of Quantisweb SAO process provided several benefits for aerodynamic system optimization when CFD calculations were performed using HPC resources. This approach permitted the generation and validation of the mathematical model immediately after the first SAO cycle. One benefit of this iterative process was to allow numerous trials at the same time in a batch-oriented way, greatly accelerating the convergence towards an ideal configuration. Within the four-week design block, the use of batch-oriented CFD runs on an HPC cluster directly contributed to a greater number of test runs. This permitted improvement in the robustness of the model, and better performance in the final aerodynamic configuration.
Conclusion:
In this paper, we presented the state of the art in mathematical simulation used in the industry. Subsequently, we presented the Quantisweb stochastic-approximation optimization methodology and software as an enabler to simulation in selecting and generating an Optimal Model and solving Problems. Finally, we introduced an example of the methodology used in a practical case where we clearly demonstrated that the cost and time to resolve a problem was drastically reduced.
REFERENCES:
[1] Mohammed S. Obaidat and Georgios I. Papadimitrium, “Applied system simulation, Methodologies and application”, Springer Science + Business Media (2003).
[2] Marie-Joelle Rochet and Jake C. Rice, “Simulation-based management strategy evolution: ignorance disguised as mathematics?” ICES- Journal of Marine Science (2009) pp 754-762.
[3] M. Arnold and al., “Numerical methods in vehicle system dynamics: State of the art and current developments.” Vehicle System Dynamics. Vol 49 (2011) pp. 1159-1207.
[4] D. Isola and A. Guardone, “Simulation of flows with strong shocks with an adaptive consecutive scheme.” Journal of Computational and Applied Mathematics. Vol 236 (2012) pp. 4660-4670.
[5] Samer Said and Mohamed Houari, “A hybrid simulation-optimization approach for the robust Discrete time /cost Trade-off Problem. Applied Mathematics and Computation.” Vol 259 (2015) pp.628-636.
[6] Jonathan Schillings and al., “Four-way coupled Eulerian-Lagrangian Direct Numerical Simulation in a vertical laminar channel flow.” International Journal of multiphase flow. Vol 89 (2017) pp.92-107.
[7] Huanzhen Chen and Hong Wang, “Numerical Simulation for conservative fractional diffusion equation by an expanded mixed formulation.” Journal of Computational and Applied Mathematics. Vol 296 (2016) pp. 480-498.
[8] Summary of the Quantisweb patent. Internal document.
[9] The Analytic Hierarchy Process, Saaty, T.L. New York, McGraw Hill. (1980).
[10] Daniel Kelly, Jessica Batty, Thomas Carrel-Billiard, Anna Cybulsky and Lucien Viala. McGill Racing Team, Montreal, Canada; Yvan Dumas, Nina Visconti and M’Hammed Mountassir. Quantisweb Technologies, Montreal, Canada. “Computational-based Aerodynamic Design for a Formula SAE Vehicle.” (2016 Article in Review).